ความรู้เบื้องต้นในการออกแบบฐานข้อมูล

การออกแบบฐานข้อมูลเป็นขั้นตอนที่สำคัญมาก ถ้าทำอย่างรอบคอบและถูกต้องจะทำให้ระบบฐานข้อมูลของงานนั้นมีความครบถ้วน ไม่ซ้ำซ้อน และมีความถูกต้อง มีผู้กล่าวว่าการออกแบบฐานข้อมูลเป็นทั้งศาสตร์และศิลป์ เพราะผู้ออกแบบฐานข้อมูลจะต้องอาศัยเทคนิคในการออกแบบประกอบกับประสบการณ์ ช่วยในการออกแบบฐานข้อมูล ในบทนี้เราจะเริ่มเรียนรู้เทคนิคในการออกแบบต่าง ๆ โดยเริ่มจากการศึกษาแนวคิดเกี่ยวกับการออกแบบฐานข้อมูล ได้แก่ แนวคิดเรื่องพจนานุกรมข้อมูล การขึ้นต่อกับแบบฟังก์ชั่น (Functional Dependencies) ซึ่งเป็นการสังเกตความสัมพันธ์ระหว่างค่าของแอตทริบิวต์ในแต่ละตารางการขึ้นต่อกันชนิดสำคัญและไม่สำคัญ สมบัติของเซตของการขึ้นต่อกัน กฎการอนุมาน เซตของการขึ้นต่อกันแบบลดรูปไม่ได้ แผนภาพการขึ้นต่อกัน (FD Diagram) และการแยกตารางย่อยออกไปโดยไม่สูญเสียคุณสมบัติที่มีอยู่เดิม (Nonloss Decomposition)

1. พจนานุกรมข้อมูล

ดังนี้ได้กล่าวไว้ในบทที่ผ่านมาว่า พจนานุกรมข้อมูล (Catalog or Data Dictionary) คือ ที่เก็บข้อมูลรายละเอียด (Detalied Information) ซึ่งที่เรียกว่าเป็น “ข้อมูลตัวอธิบาย” (Descriptor Information) หรือ “ข้อมูลที่เกี่ยวกับข้อมูล” (Metadata) เช่น

TEBLE

ตารางข้างตนนี้เก็บข้อมูลเกี่ยวกับตารางในระบบว่ามีตารางชื่ออะไรบ้าง (TABLE NAME TABNAME) แต่ตารางมีจำนวนคอลัมน์หรือสดมภ์หรือแอตทริบิวต์เท่าใด (COLCOUNT) แต่ละตารางมีข้อมูลที่แถวหรือกี่ทูเพิล (ROWCOUNT) และคำอธิบายเกี่ยวกับตาราง (DESCRIPTION) เป็นต้น

COLUMN

ตารางข้างต้นนี้เก็บข้อมูลแอตทริบิวต์ในตารางว่ามีชื่อแอตทริบิวต์อะไร โครงสร้างข้อมูล ความกว้างของตข้อมูล คีย์หลัก คีย์นอก และตารางอ้างอิงของคีย์นอก เป็นต้น
พจนานุกรมหรือแค็ตตาล็อกนี้เป็นที่ซึ่ง เค้าร่าง (Schemas) ทั้งหลาย ไม่ว่าจะเป็นร่างภายนอก เค้าร่างภายใน รวมทั้งการเชื่อมระหว่างระดับ (การเชื่อมระหว่างระดับภายนอกกับระดับแนวคิด หรือการเชื่อมระหว่างระดับแนวคิดกับระดับภายใน) ถูกนำมาเก็บไว้ กล่าวได้ว่าพจนานุกรมเก็บข้อมูลรายละเอียดที่เกี่ยวกับวัตถุต่าง ๆ ที่เป็นประโยชน์ต่อระบบเองในการทำงาน วัตถุดังกล่าวก็อย่างเช่น เรลวาร์, ดัชนี, ผู้ใช้, ข้อกำหนดความคงสภาพ (Integrity Constraints), ข้อกำหนดเรื่องความปลอดภัย, และอื่น ๆ เป็นต้น
โดยปรกติแล้วระบบบริหารฐานข้อมูลจะมีหน้าที่จัดทำพจนานุกรมข้อมูล หรือแค็ตตาล็อก ให้แก่ผุ้ใช้ พจนานุกรมข้อมูลที่ระบบบริหารฐานข้อมูลสร้างขึ้นให้โดยนี้เรียกว่า พจนานุกรมข้อมูลแบบแอคทีฟ (Active Data Dictionary) ที่ผู้ใช้สามารถขอดูได้โดยใช้คำสั่งต่าง ๆ ดังที่อธิบายไว้ในท้ายบทที่แล้ว
ส่วนพจนานุกรมข้อมูลที่ผู้บริหารฐานข้อมูลแบบแพสสีฟ (Passive Data Dictonary) ซึ่งอาจมีลักษณะรายละเอียดปลีกย่อยแตกต่างกันไป ตัวอย่างเช่น พจนานุกรมข้อมูลของตารางที่ชื่อว่า FEE_PRICE ซึ่งเป็นตารางหนึ่งในระบบงานฐานข้อมูลทะเบียนนักศึกษา มีลักษณะและรูปแบบในการจัดเก็บ ดังนี้

*PK หมายถึง คีย์หลัก (Primary Key)
*FK หมายถึง คีย์นอก (Foreign Key)
*xxx หมายถึง ตัวอักขระอะไรที่นำมาเก็บไว้โดยไม่มีการนำไปคำนวณ
สรุปได้ว่ารายละเอียดพื้นฐานต่าง ๆ ที่ควรจะเก็บไว้ในพจนานุกรมข้อมูล ในกรณีที่นักวิเคราะห์และออกแบบระบบจัดทำเอง หรือการจักทำพจนานุกรมแบบแพสสีฟ ก็คือ รายละเอียดทุก ๆ อย่างที่น่าจะเป็นประโยชน์ต่อการพัฒนาระบบฐานข้อมูลนั้นทั้งหมด โดยควรจัดจัดเก็บไว้ให้ได้มากที่สุดเท่าที่จะทำได้ เช่น

1. ชื่อตารางหรือรีเลชั่น และคำอธิบาย (ถ้าจำเป็น)
2. ชื่อแอตทริบิวต์ หรือโดเมน และคำอธิบาย (ถ้าจำเป็น)
3. ชื่อคีย์หลัก, คีย์ประกอบ, คีย์คู่แข่ง หรือคีย์เผื่อเลือก
4. ชือคีย์นอก
5. ชนิดของข้อมูล
6. ขนาดความกว้างของข้อมูล
7. พิสัยของข้อมูล
8. ตัวอย่างข้อมูล
9. ดัชนี หรือการระบุว่าจะเก็บค่าว่างในแอตทริบิวต์นั้นได้หรือไม่
10. ชื่อระบบฐานข้อมูล หรือโครงการ
11. หมายเลขลำดับตาราง
12. หมายเลขลำดับของแอตทริบิวต์
13. อื่น ๆ

1. การเชื่อมต่อกันแบบฟังก์ชั่น

การเชื่อมต่อกันแบบฟังก์ชั่น (Functional Dependencies) ซึ่งต่อไปจะเรียกอย่างย่อว่า การขึ้นต่อกัน เป็นสัมพันธภาพจากเซตของแอตทริบิวต์หนึ่งไปยังอีกเซตหนึ่งในลักษณะหลายต่อหนึ่ง (many –to-one relationship) ภายในตารางเดียวกัน เช่น ในตาราง SP มีแอตทริบิวต์ SNO และ PNO สมัพันธ์กับ OTY

SP
ในตารางนี้ SP มีการขึ้นต่อกันจากเซตของแอตทริบิวต์แรก คือ {SNO, PNO} ไปยังเซตของแอตทริบิวต์ที่สองคือ {QTY} ซึ่งหมายความว่าในตารางใดที่มีค่าข้อมูลที่ถูกต้อง แล้ว...
• ค่าที่กำหนดให้ของคุ่ {SNO, PNO} จะมีค่า {QTY} ที่สอดคล้องกันเพียงค่าเดียวเท่านั้น เช่น {S1, P1} จะสอดคล้องคุ่กับ {300} เท่านั้น
• ค่าของ {SNO, PNO} ที่แตกต่างกันหลายค่า อาจมีค่า {QTY} ที่เป็นค่าเดียวกันได้ เช่น {S1, P1} {S2, P1} และ {S4, P4} ต่างมีค่า {QTY} สอดคล้องกัน คือ {300}
เราอาจให้ค่าจำกัดความว่า
Y is functionally dependent on X หรือ X functionally determines Y
ก็ต่อเมื่อ แต่ละค่าของ X จะมีค่า Y ที่สอดคล้องหรือเกี่ยวข้องกับ X เพียงค่าเดียวเท่านั้น ซึ่งนิยมเขียนเป็นสัญลักษณ์ว่า
X g Y
ในกรณีของตาราง SP เราจึงพบว่า
{SNO, PNO} g QTY
ซึ่งสิ่งที่พึ่งประสงค์ คือ การทำให้เหลือเซตที่เล็กที่สุดซึ่งแทนการขึ้นต่อกันได้ทั้งหมด ดังเช่นกรณีของ ตาราง P ต่อไปนี้

P

จะพบว่ามีการขึ้นต้นกันดังต่อไปนี้
PNO g PNO
PNO g PNAME
PNO g COLOR
PNO g WEIGHT
PNO g CITY
ซึ่งสามารถสรุปรวมได้เป็นเซตเดียวกัน คือ
PNO g {PNO, PNAME, COLOR, WEIGHT, CITY}
อีกอย่างหนึ่งต่อไปนี้ ถ้าเรากำหนดให้มีตาราง SCP เก็บ SNO (เลขรหัสผั้ดส่งสินค้า) CITY (เมืองที่อยู่ของผู้จัดส่งสินค้า) PNO (เลขรหัสประเภทสินค้า) QTY (จำนวนของสินค้าที่จัดส่งแต่ละครั้ง) และมีค่าข้อมูล ด้งนี้

SCP
จะพบว่ามีการขึ้นต่อกันดังต่อไปนี้
{SNO, PNO} g QTY
{SNO, PNO} g CITY
{SNO, PNO} g {CITY, QTY}
{SNO, PNO} g {SNO}
{SNO, PNO} g {SNO, PNO, CITY, QTY}
{SNO} g CITY
เราจะพบว่าตารางนี้ไม่สามารถจะทำให้เกิดเซตที่เล็กที่สุดของการขึ้นต่อกันได้ แสดงว่ามีบางอย่างไม่ดีนักในการกำหนดตารางรางดังกล่าวนี้ ซึ่งก็คือ เกิดมีความซ้ำซ้อน (Redundancy) ในการเก็บข้อมูลของฐานข้อมูลนี้ เนื่องจากในบรรทัดสุดท้ายมีการขึ้นต่อกันที่แตกต่างจากบรรทัดอื่น ๆ ก่อนหน้า กล่าวคือ SNO ไม่ใช่คีย์หลัก (Primary Key) และไม่ใช่คีย์คู่แข่ง (Candidate Kdy) ซึ่งถ้าพจน์ที่อยู่ทางด้านซ้ายไม่ใช้คีย์หลัก หรือคีย์คู่แข่งแล้วจะเกิดความซ้ำซ้อนขึ้นในฐานข้อมูล ฉะนั้นในการออกแบบฐานข้อมูลควรกำจัดลักษณะของการขึ้นต่อกันอย่างบรรทัดสุดท้ายดังกล่าวออกไป

1. การขึ้นต่อกันชนิดสำคัญและไม่สำคัญ

การขึ้นต่อกันชนิดสำคัญหรือไม่ใช่เรื่องเล็กน้อย (Nontrivial Dependencies) และการขึ้นต่อกันชนิดไม่สำคัญหรือเป็นเรื่องเล็กน้อย (Trivial Dependencies) มีลักษณะดังต่อไปนี้
การขึ้นต่อกันจะถือเป็นชนิดไม่สำคัญ ก็ต่อเมื่อตัวที่อยู่ทางด้านขวามือเป็นสับเซตของตัวที่อยู่ทางซ้ายมือ เช่น
จากตาราง SCP ข้างต้น มีการขึ้นต่อกันตัวหนึ่ง คือ
{SNO, PNO} g SNO
ซึ่งถือว่าเป็นการขึ้นต่อกันชนิดไม่สำคัญเพราะ SNO เป็นสับเซตของ {SNO, PNO} และจากตาราง P ข้างต้น มีการขึ้นต่อกันอีกตัวหนึ่งคือ
PNO g PNO
ซึ่งถือเป็นการขึ้นต่อกันชนิดไม่สำคัญเพราะ PNO เป็นสับเซตของ PNO แม้จะไม่ใช่สับเซตที่เหมาะสม (Proper Subset) ก็ตาม
ส่วนการขึ้นต่อกันชนิดสำคัญ เป็นสิ่งที่เราสนใจในการออกแบบระบบฐานข้อมูล เพราะเป็นสิ่งที่ตรงกับข้อกำหนดเรื่องความคงสภาพหรือความถูกต้อง (Integrity Constraints) ที่แท้จริงเช่น
จากตาราง SCP ข้างต้น มีการขึ้นต่อกันชนิดสำคัญได้แก่
{SNO, PNO} g QTY
{SNO, PNO} g CITY
{SNO} g CITY
จากตาราง P ข้างต้น มีการขึ้นต่อกันชนิดสำคัญได้แก่
PNO g PNAME
PNO g COLOR
PNO g WEIGHT
PNO g CITY
ในการออกแบบระบบฐานข้อมูลเราจะสนใจเฉพาะการขึ้นต่อกันที่สำคัญเท่านั้น และจะพยายามตัดทิ้งการขึ้นต่อกันชนิดไม่สำคัญออกไป เพื่อให้ได้เซตที่เล็กที่สุด ทั้งนี้เพราะให้เกิดความสะดวกในการสร้างข้อกำหนด หรือข้องบังคับ (Constraint) ในระบบฐานข้อมูลของเรา

1. แผนภาพการขึ้นต่อกัน

แผนการขึ้นต่อกัน หรือ Functional Dependency Diagram เป็นวิธีแสดงให้เห็นภาพการขึ้นต่อกันให้เห็นได้ง่าย ชัดเจนและสะดวก โดยใช้กรอบสี่เหลี่ยมผืนผ้าแทนแอตทริบิวต์แต่ละตัว และใช้ลูกศรชี้ออกจากคีย์ (Candidate Keys หรือ Primary Keys) ซึ่งจะทำให้สะดวกในการออกแบบให้ตารางอยู่ในรูปปกติโดยการตัดลูกศรที่ทำให้เกิดปัญหาหรือสร้างความยุ่งยากออกไป
ตัวอย่าง จากตาราง SCP ซึ่งมีการขึ้นต่อกัน คือ
{SNO, PNO} g QTY
SNO g CITY
เราสามรถแสดงด้วยแผนภาพการขึ้นต่อกันเป็นดังนี้
(C.J. Date, 2000)




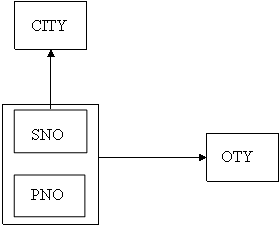
หรือแสดงด้วยแผนภาพการขึ้นต่อกันอย่างง่าย (ดัดแปลงจาก Kendall and Kendall, 1999 และ สุวัตร ปัทมวรคุณ, 2544) เป็นดังนี้




ตัวอย่าง จากตาราง P ซึ่งมีการขึ้นต่อกัน คือ
PNO g PNAME
PNO g COLOR
PNO g WEIGHT
PNO g CITY
เราสามารถแสดงด้วยแผนภาพขึ้นต่อกันเป็นดังนี้



หรือแสดงด้วยแผนภาพการขึ้นต่อกันอย่างง่ายเป็นดังนี้

1. สมบัติปิดของเซตของการขึ้นต่อกัน

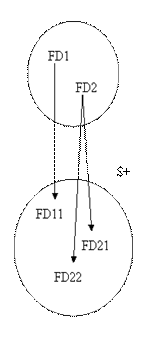
สมบัติของเซตของการขึ้นต่อกัน (Closure of a Set of Dependencies) คือ เซตของการขึ้นต่อกันทั้งหมดที่ถูกบ่งชี้โดยเซต S ของการขึ้นต่อกัน ซึ่งสมบัตินี้จะแทนด้วย S+ (The set of all FDs that are implied by a given set S of FDs is called the closure of S, written S+ ) กล่าวคือ หากการขึ้นต่อกันข้อใดก็ตามเป็นผลมาจากการบ่งชี้หรือการระบุของการขึ้นต่อกันในเซต S แล้ว เราถือว่าการขึ้นต่อกันทุกข้อดังกล่าวอยู่ในเซต S+ ซึ่งก็คือ สมบัติปิดของเซตของการขึ้นต่อกันนั่งเอง ดังภาพ
ในภาพข้างบนแสดงให้เห็นว่า เซต S มีการขึ้นต่อกันอยู่ 2 นิพจน์คือ FD1 และ FD2 โดยที่ FD1 บ่งชี้ว่ามีการขึ้นต่อกันอย่าง FD11 และ FD2 บ่งชี้ว่ามีการขึ้นต่อกันอย่าง FD21 และ FD22 ดังนั้น FD11, FD21 และ FD22 จะจัดอยู่ในเซต S+ ซึ่งเป็นสมบัติของเซต S ตัวอย่างจากตารางที่ผ่านมา เช่น การขึ้นต่อกันที่กำหนดว่า
{SNO, PNO} g {CITY, QTY}
จะบ่งชี้ว่าทำให้มี การขึ้นต่อกันอีกสองนิพจน์ซึ่งเป็นสมบัติปิดของมัน ได้แก่
{SNO, PNO} g CITY
{SNO, PNO} g QTY

1. กฎการอนุมาน

กฎการอนุมาน (Inference Rules) เป็นกฎที่เกี่ยวเนื่องจากเรื่องสมบัติปิดของเซตการขึ้นต่อกันกฎนี้เรียกว่า กฎของอาร์เรย์สตรอง (Armstrong’s Axioms) ตามชื่อของ W. W'. Armstrong ผู้คิดขึ้นมาเมื่อปี ค.ศ. 1974 ซึ่งเป็นกฎที่บ่งชี้การได้มาของสมบัติของเซตการขึ้นต่อกัน (Derive Closure S+) กฎดังกล่าวมีสาระหลักอยู่ 3 ข้อแรก ส่วนข้ออื่น ๆ ประยุกต์ต่อจาก 3 ข้อแรก ดังต่อไปนี้

1. กฎการสะท้อน (Reflexivity) กล่าวว่า ถ้า B เป็นสับเซตของ A แล้ว A g B
2. กฎเสริม (Augmentation) กล่าวว่า ถ้า A g B แล้ว AC g BC
3. กฎถ่ายทอด (Transitivity) กล่าวว่า ถ้า A g B และ B g C แล้ว A g C ซึ่งกล่าวอีกอย่างหนึ่งได้ว่า A g C ผ่านทาง B
4. กฎกำหนดตนเอง (Self-determination) กล่าวว่า A g A
5. กฎการแยกส่วน (Decomposition) กล่าวว่า ถ้า A g BC แล้ว A g B

และ A g C

1. กฎการรวม (Union) กล่าวว่า ถ้า A g B และ A g C แล้ว A g BC
2. กฎการประกอบ (Composition) กล่าวว่า ถ้า A g B และ C g D

แล้ว AC g BD

1. กฎการรวม (Union) กล่าวว่า ถ้า A g B และ A g C แล้ว A g BC
2. กฎการประกอบ (Composition) กล่าวว่า ถ้า A g B และ C g D

แล้ว AC g BD

1. ทฤษฎีบทเอกภาพทั่วไป (General Unification Theorem) ซึ่งพิสูจน์โดย ดาร์เวน (Darwen, 1992) กล่าวว่า ถ้า A g B และ C g D แล้ว A U (C - B) g BD

ตัวอย่าง ให้ R (A, B, C, D, E, F) และมีการขึ้นต่อกัน ดังนี้
A g BC
B g E
CD g EF
จากแสดงว่า การขึ้นต่อกัน FD – AD g F เป็นสมาชิกของสมบัติของเซตนี้
วิธีทำ
1. A g BC (กำหนดให้)
2. A g C (กฎการแยกส่วน)
3. AD g CD (กฎเสริม)
4. CD g EF (กำหนดให้)
5. AD g F (กฎการแยกส่วน)

1. เซตของการขึ้นต่อกันซึ่งได้ลดรูปไม่ได้

เซตของการขึ้นต่อกันซึ่งลดรูปไม่ได้ (Inreducible sets of dependencies) คือ เซตของการขึ้นต่อกันที่มีการตัดหรือลด การขึ้นต่อกันที่ไม่จำเป็นหรือไม่สำคัญออกไป กล่าวคือ ถ้าให้ S1 และ S2 เป็นเซตของการขึ้นต่อกัน 2 เซต
• ถ้าการขึ้นต่อกันทุกนิพจน์ที่ถูกระบุโดย S1 ได้มาจากการระบุโดย S2 อีกทอดหนึ่ง เช่น ถ้า S1+ เป็นสับเซตของ S2+ แล้ว เรากล่าวว่า S2 เป็นตัวครอบคลุม (Cover) สำหรับ S1 หรือเรียกสั้น ๆ ว่า S2 คลุม S1
• ถ้า S2 เป็นตัวครอบคลุมสำหรับ S1 และ S1 ก็เป็นตัวครอบคลุมสำหรับ S2 ด้วยแล้วเราเรียกว่า S1 และ S2 เท่าเทียมกัน (S1 and S2 are equivalent.) เช่น S1+=S2+ เซตการขึ้นต่อกัน S จะเป็นเซตที่ลดรูปไม่ได้ก็ต่อเมื่อมีสมบัติ 3 ประการ ดังนี้
1. ด้านขวาของการขึ้นต่อกันทุกตัวในเซต S เป็นแบบแอตทริบิวต์เดียว คือ เป็น เซตเดี่ยว (Singleton Set)
2. ด้านซ้ายมือของการขึ้นต่อกัน ถ้าเป็นเซตของคีย์หลักหลายตัวจริงจะต้องไม่สามารถตัดเอาตัวใดตัวหนึ่งออกไปได้เพราะ จะทำให้ไม่สมบูรณ์ (Left-irreducible) เช่น
{SNO, PNO, X} g QTY
3. การขึ้นต่อกันใด ๆ ในเซต S จะตัดหรือลดเอาตัวใดตัวหนึ่งออกไป โดยความหมายไม่เปลี่ยนไม่ได้ กล่าวอีกนัยหนึ่ง หากเซตใดเป็นเซตที่ลดรูปไม่ได้แล้วย่อมหมายความว่าจะตัดเอาการขึ้นต่อกันนิพจน์ใดนิพจน์หนึ่งออกไม่ได้ มิฉะนั้นความหมายจะขาดหายไม่ครบถ้วน
ตัวอย่าง 1 ถ้าตาราง P มีการขึ้นต่อกันดังนี้ คือ
PNO g PNAME
PNO g COLOR
PNO g WEIGHT
PNO g CITY
วิธีคิด เซตของการขึ้นต่อกันข้างต้นเป็นเซตที่ลดรูปไม่ได้อีกแล้ว เพราะทางด้านขวาเป็นแอตทริบิวต์เดี่ยวในแต่ละบรรทัด ส่วนทางด้านซ้ายก็เป็นเช่นเดียวกันไม่สามารถตัดทอนได้อีก นอกจากนั้นการขึ้นต่อกันแต่ละนิพจน์ดังกล่าวก็ไม่สามารถตัดขึ้นบรรทัดใดได้ เพราะจะทำให้ความหมายเปลี่ยนสมบัติปิด
ตัวอย่างที่ 2 ถ้าตาราง P มีการขึ้นต่อกันดังนี้ คือ
PNO g {PNAME, COLOR}
PNO g WEIGHT
PNO g CITY
วิธีคิด เซตของการขึ้นต่อกันข้างต้นเป็นเซตที่ลดรูปได้อีก เพราะนิพจน์ของการขึ้นต่อกันในบรรทัดแรก มีนิพจน์ด้านขวาไม่เป็น Singleton Set
ตัวอย่างที่ 3 ถ้าตาราง P มีการขึ้นต่อกันดังนี้
{PNO, PNAME} g COLOR
PNO g PNAME
PNO g WEIGHT
PNO g CITY
วิธีคิด เซตของการขึ้นต่อกันข้างต้นเป็นเซตที่ลดรูปได้อีก เพราะนิพจน์ของการขึ้นต่อกันในบรรทัดแรกมีนิพจน์ด้านซ้ายไม่เป็น Singleton Set และเราสามารถตัด PNAME ออกไปจากนิพจน์ด้านซ้ายนั้นได้โดยสมบัติปิดไม่เปลี่ยนแปลงไป
ตัวอย่างที่ 4 ถ้าตาราง P มีการขึ้นต่อกันดังนี้ คือ
PNO g PNO
PNO g PNAME
PNO g COLOR
PNO g WEIGHT
PNO g CITY
วิธีคิด เซตของการขึ้นต่อกันข้างต้นเป็นเซตที่ลดรูปได้อีก เพราะนิพจน์ของการขึ้นต่อกันในบรรทัดแรกนั้นเราสามารถตัดทิ้งออกได้ทั้งบรรทัด โดยสมบัติปิดไม่เปลี่ยนแปลงไป
การพยายามสร้างเซตของการขึ้นต่อกันซึ่งลดรูปไม่ได้ขึ้นมานั้นก็เพื่อจะได้นำไปสร้างข้อกำหนดหรือข้อบังคับ (Constraint) ที่มีจำนวนน้อยที่สุดเพื่อประหยัดเวลา แรงงานโปรแกรมเมอร์ และพลังงานการทำงานของเครื่องคอมพิวเตอร์

1. การแยกตารางโดยไม่สูญเสียความหมาย

การแยกตารางโดยไม่สูญเสียความหมายเดิม (Nonloss Decomposition) คือ การแยกตารางเดิมตารางหนึ่งออกไปเป็นหลายตารางโดยไม่สูญเสียคุณสมบัติที่มีอยู่ในตารางเดิม เป็นวิธีการสำคัญอย่างหนึ่งในการทำให้ฐานข้อมูลอยู่ในรูปแบบปรกติหรือบรรทัดฐาน (Normal Form) ซึ่งจะได้เรียนรู้รายละเอียดในหน่วยเรียนถัดไป ก่อนอื่นควรทำความเข้าใจกับการแยกตารางเสียก่อน
การแยกตาราง (Decomposition) เป็นการทำ Projection อย่างหนึ่ง กล่าวคือ เป็นการดึงคอลัมน์ของข้อมูลเฉพาะบางคอลัมน์ออกมาจากตารางที่มีอยู่เดิม แล้วนำไปสร้างเป็นตารางใหม่ขึ้นมาหลายตารางตาความต้องการ ตัวอย่างเช่น ถ้าเดิมมีการออกแบบโดยกำหนดให้มีตาราง SCP พร้อมข้อมูล ดังนี้

SCP
จะพบว่ามีการขึ้นต่อกันเฉพาะที่สำคัญดังต่อไปนี้
{SNO, PNO} g QTY
SNO g CITY
(ในที่นี้ เราตัด {SNO, PNO} g CITY ทิ้งไปเพราะเป็นการขึ้นต่อกันที่ซ้ำซ้อนกับ SNO g CITY ทีมีอยู่แล้ว ตามหลักการของ การขึ้นต่อกันแบบด้านซ้ายลดรูปไม่ได้ หรือ Left-irreducible FDs)
จะเห็นได้ว่าตารางนี้มีการเก็บข้อมูลแต่ละทูเพิล (Tuple) เป็นค่าเดียว (Atomic) อยู่แล้ว กล่าวอีกนัยหนึ่งคือ อยู่ในรูปแบบปรกติระดับที่ 1 (Pirst Normal Form) แล้ว แต่ยังมีความไม่เรียบร้อยอยู่บางอย่าง คือ ยังเป็นการกำหนดการแบ่งตารางที่ไม่ดีนักเพราะเก็บข้อมูลหลายเรื่องไว้ในตารางเดียวกัน ซึ่งจะทำให้เกิดปัญหาการเก็บข้อมูลซ้ำซ้อน (Redundancy) และปัญหาความผิดปกติในการปรับปรุงข้อมูล (Update Anomaly) เมื่อทราบข้อบกพร่องดังนี้จึงจะต้องแก้ปัญหาโดยการแยกตาราง SCP นี้ย่อยออกเป็นสองตารางซึ่งมีทางเลือก ดังนี้
ทางเลือกที่ 1 จาก SCP (SNO, CITY, PNO, QTY) แยกเป็น
SC (SNO, CITY) และ
SP (SNO, PNO, QTY)

ทางเลือกที่ 2 จาก SCP (SNO, CITY, PNO, QTY) แยกเป็น
SPC (SNO, PNO, CITY) และ
SQ (SNO, QTY)
การจะเลือกทางใดนั้นต้องพิจารณาว่าหลังจากที่ทำการแยกตารางออกไปแล้ว เราสามารถทำย้อนกลับ คือ เอาตารางใหม่ทั้งสองตารางมารวมกัน (JOIN) เพื่อให้ได้ข้อมูลอย่างตารางเดิมได้หรือไม่ ถ้าไม่สามารถทำได้แสดงว่าเกิดการสูญเสียลักษณะการขึ้นต่อกันบางอย่างไป กาออกแบบฐานข้อมูลที่ดี จึงต้องทำให้ตารางที่แยกออกมาใหม่นั้นสามารถรักษาคุณสมบัติการขึ้นต่อกันที่มีอยู่เดิมเอาไว้ให้ได้
กรณีเลือกทางที่ 1 จะได้ตารางพร้อมข้อมูล ดังนี้

SC

SP
จะพบว่าตาราง SC มีการขึ้นต่อกันที่สำคัญ คือ
SNO g CITY
และพบว่าตาราง SP มีการขึ้นต่อกันที่สำคัญ คือ
{SNO, PNO} g QTY
กรณีเลือกทางที่ 2 จะได้ตารางสองตารางพร้อมข้อมูล ดังนี้

SPC

SQ
จะพบว่าตาราง SPC มีการขึ้นต่อกันที่สำคัญ คือ
SNO g CITY
{SNO, PNO} g CITY
และพบว่าตาราง SQ มีการขึ้นต่อกันที่สำคัญ คือ
{SNO, QTY} g QTY
สรุป จะพบว่าทางเลือกที่ 1 ดีกว่าทางเลือกที่ 2 เพราะ
1. สามารถรักษาสมบัติการขึ้นต่อกันซึ่งมีอยู่แต่เดิมเอาไว้ได้ทั้งหมด คือทั้ง
{SNO, PNO} g QTY และ
{SNO} g CITY
2. ไม่มีนิพจน์การขึ้นต่อกันที่เกินเข้ามาอย่างทางเลือกที่ 2 ซึ่งเป็นการทำให้ความหมายดังเดิมของฐานข้อมูลผิดเพี้ยนไป
3.ทางเลือกที่ 2 ทำให้ขาดคุณสมบัติการขึ้นต่อกันไปประการหนึ่ง คือ
{SNO, PNO} g QTY